Providence, RI--- In the 19th century, Lord Kelvin made the inspiredguess that elements are knots in the "ether". Hydrogen would be onekind of knot, oxygen a different kind of knot---and so forththroughout the periodic table of elements. This idea led PeterGuthrie Tait to prepare meticulous and quite beautiful tables ofknots, in an effort to elucidate when two knots are truly different.From the point of view of physics, Kelvin and Tait were on the wrongtrack: the atomic viewpoint soon made the theory of ether obsolete.But from the mathematical viewpoint, a gold mine had been discovered:The branch of mathematics now known as "knot theory" has beenburgeoning ever since.
In his article "The Combinatorial Revolution in Knot Theory", to appear in the December 2011 issue of the Notices of the AMS,, SamNelson describes a novel approach to knot theory that has gainedcurrency in the past several years and the mysterious new knot-likeobjects discovered in the process.
As sailors have long known, many different kinds of knots arepossible; in fact, the variety is infinite. A *mathematical* knot canbe imagined as a knotted circle: Think of a pretzel, which is aknotted circle of dough, or a rubber band, which is the "un-knot"because it is not knotted. Mathematicians study the patterns,symmetries, and asymmetries in knots and develop methods fordistinguishing when two knots are truly different.
Mathematically, one thinks of the string out of which a knot is formedas being a one-dimensional object, and the knot itself lives inthree-dimensional space. Drawings of knots, like the ones done byTait, are projections of the knot onto a two-dimensional plane. Insuch drawings, it is customary to draw over-and-under crossings of thestring as broken and unbroken lines. If three or more strands of theknot are on top of each other at single point, we can move the strandsslightly without changing the knot so that every point on the planesits below at most two strands of the knot. A planar knot diagram isa picture of a knot, drawn in a two-dimensional plane, in which everypoint of the diagram represents at most two points in the knot.Planar knot diagrams have long been used in mathematics as a way torepresent and study knots.
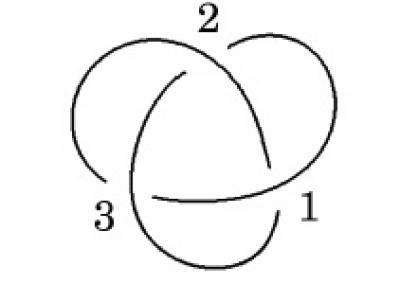
This knot has Gauss code O1U2O3U1O2U3.
(Photo Credit: Graphic by Sam Nelson.)
As Nelson reports in his article, mathematicians have devised variousways to represent the information contained in knot diagrams. Oneexample is the Gauss code, which is a sequence of letters and numberswherein each crossing in the knot is assigned a number and the letterO or U, depending on whether the crossing goes over or under. TheGauss code for a simple knot might look like this: O1U2O3U1O2U3.
In the mid-1990s, mathematicians discovered something strange. Thereare Gauss codes for which it is impossible to draw planar knotdiagrams but which nevertheless behave like knots in certain ways. Inparticular, those codes, which Nelson calls *nonplanar Gauss codes*,work perfectly well in certain formulas that are used to investigateproperties of knots. Nelson writes: "A planar Gauss code alwaysdescribes a [knot] in three-space; what kind of thing could anonplanar Gauss code be describing?" As it turns out, there are"virtual knots" that have legitimate Gauss codes but do not correspondto knots in three-dimensional space. These virtual knots can beinvestigated by applying combinatorial techniques to knot diagrams.
Just as new horizons opened when people dared to consider what wouldhappen if -1 had a square root---and thereby discovered complexnumbers, which have since been thoroughly explored by mathematiciansand have become ubiquitous in physics and engineering---mathematiciansare finding that the equations they used to investigate regular knotsgive rise to a whole universe of "generalized knots" that have theirown peculiar qualities. Although they seem esoteric at first, thesegeneralized knots turn out to have interpretations as familiar objectsin mathematics. "Moreover," Nelson writes, "classical knot theoryemerges as a special case of the new generalized knot theory."
Source: American Mathematical Society